Бінарне кодувння інформації

Будь-яка інформація усередині комп'ютера зберігається і обробляється у вигляді довгого коду, що складається всього з двох символів. Цей код називається двійковим чи бінарним.

За своєю суттю він дуже схожий на всім відомий код Морзе, у якому двома символами (довгий і короткий імпульс) шифруються літери для передачі текстової інформації по дротах або іншим способом.

Комп'ютери ж пішли значно далі. В них у формі бінарного коду зберігаються не лише текстові дані, але й програми, музика, зображення і навіть відео високої чіткості.

Перед виведенням інформації на екран, в аудіосистему або роздруковуванням, комп'ютер "перекладає" її на зрозумілу людині мову. Але всередині комп'ютера вона зберігається і обробляється виключно у вигляді двійкового коду.

Якщо ви не програміст, знати систему використання бінарного коду досконало не обов'язково. Для розуміння принципів роботи комп'ютера достатньо розібратися з питанням у загальних рисах. В цьому вам і допоможе пропонована стаття.

Зміст статті

Чому в комп'ютері використовується бінарний код

Люди для запису текстової інформації використовують букви. В українській мові їх 33. Комбінаціями з десяти цифр (від 0 до 9) ми записуємо числові дані. При роботі з графічною інформацією користуємося палітрою з мільйонів кольорів. Наші вуха розрізняють звуки в діапазоні від 16 до 20000 Гц.

Якщо додати до цього нюх, смакові та тактильні відчуття, отримаємо величезне різноманіття інформаційних імпульсів, які може сприймати, зберігати і обробляти наш мозок.

За допомогою технічних засобів неможливо відтворити аналогічну систему роботи з інформацією.

Людям найлегше створювати прилади, які приймають один із двох станів: лампочка горить або ні, магнітне поле є або його немає і т.д. І значно складніше, наприклад, змусити лампочку в різних ситуаціях світитися одним з 10 кольорів. Не кажучи вже про 10 мільйонів кольорів, які розпізнаються людиною.

У техніці значно зручніше мати справу з великою кількістю простих елементів, ніж з незначною кількістю складних.

Ідея використання бінарного коду належить німецькому математику Готфріду Лейбніцу (1646 - 1716).
Він розробив двійкову арифметику і навіть створив креслення бінарної обчислювальної машини, однак не зумів її побудувати.

Щоб мати можливість зберігати і обробляти інформацію технічними засобами, люди вирішили перекладати її на максимально просту "мову", яка складається лише з двох "літер", - так званий двійковий або бінарний код.

Використовуючи різні комбінації великої кількості двох символів, у бінарному коді можна зашифрувати будь-яку числову, текстову, звукову або графічну інформацію.

Комп'ютер же є нічим іншим, як машиною, призначеною для зберігання і обробки інформації у такому вигляді.

Переведення даних у бінарний код називається кодуванням.

Протилежний процес, в результаті якого бінарний код перетворюється на звичну для людей інформацію, називається декодуванням.

Комп'ютер здійснює кодування "на льоту" при отриманні даних ззовні: введення тексту користувачем з клавіатури, запис відео з веб-камери, запис звуку з мікрофону і т.д.

Перед виведенням інформації на екран, в аудіосистему або ж її роздруковуванням, відбувається зворотний процес (декодування).

Як здійснюється кодування різних типів даних, розглянемо трохи нижче. Спочатку давайте розберемося, з яких же символів формується двійковий код усередині комп'ютера і як він там зберігається.

З технічного боку комп'ютерний бінарний код реалізується наявністю або відсутністю певних властивостей (імпульсів) у найдрібніших запам'ятовуючих елементів. Ці імпульси можуть бути:

• фотооптичними

Так, поверхня будь-кого оптичного диску (CD, DVD або BluRay) складається зі спіралі, яку формують дрібні відрізки. Кожен з них може бути або темного або світлого кольору. Диск швидко обертається в дисководі. На його спіральній доріжці фокусується лазер, відображення якого потрапляє на фотоелемент. Темні ділянки спіралі поглинають світло і не передають його на фотоелемент, світлі - навпаки, відбиваючи світло, передають імпульс фотоелементу. В результаті фотоелемент отримує інформацію, зашифровану в доріжці диска у вигляді темних і світлих відрізків.

• магнітними

Наприклад, усередині жорсткого диска знаходиться пластина, що швидко обертається. Уся її поверхня теж є спіраллю, яка складається з послідовності мільйонів дрібних ділянок. Кожна з них є елементом, який може приймати один із двох станів: "намагнічений", "ненамагнічений". Ці елементи і формують двійковий код, в якому кодується якась інформація. Зчитування стану елементів здійснюється спеціальною головкою, яка швидко рухається по поверхні пластини;

• електричними

Наприклад, оперативна пам'ять комп'ютера є мікросхемою, що складається з мільйонів маленьких блоків, створених з мікроскопічних транзисторів і конденсаторів. Кожен такий блок може або містити електричний заряд, або ні. Комбінації заряджених і розряджених елементів оперативної пам'яті і формують в ній двійковий код.

У аналогічній формі інформація зберігається й в усіх інших запам'ятовуючих мікросхемах (флешки, SSD-носії та ін.).

Процесор комп'ютера обробляє двійковий код теж у вигляді електричних імпульсів.

Іноді можна зустріти хибну думку, що бінарний код усередині комп'ютера записаний у вигляді звичайних нулів та одиниць. Це наслідок нерозуміння технічної сторони питання. Звичних для нас нулів і одиниць в комп'ютері немає. "Символами" комп'ютерного двійкового коду є наявність або відсутність у найдрібнішого запам'ятовуючого елемента певної властивості (див. вище).

Щоб було наглядніше, в учбових матеріалах відсутність у елемента такої властивості лише умовно позначають нулем, а її наявність - одиницею. Але з таким же успіхом їх можна б було позначати крапкою і тире або хрестиком і нуликом.

Одиниці комп'ютерної інформації

У попередньому пункті вже йшлося про те, що бінарний код усередині комп'ютера зберігається у вигляді комбінацій великої кількості елементів, кожен з яких може мати один з двох станів.

Такий найдрібніший елемент, що бере участь у формуванні бінарного коду, називається бітом.

Бітом є, наприклад, кожна темна або світла ділянка доріжки оптичного диска, кожен запам'ятовуючий блок оперативної пам'яті комп'ютера і т.д.

Чим більше бітів містить якийсь носій, тим більше інформації на ньому можна закодувати. Приміром, оптичний диск типу "CD" може містити близько 6 млрд. бітів. Жорсткий диск - у десятки разів більше.

Однак кожен окремий біт сам по собі не має практичної цінності. Для кодування інформації використовуються блоки з декількох бітів.

Уявімо, наприклад, що в якомусь запам'ятовуючому пристрої міститься тільки один біт. У ньому можна буде закодувати лише один з двох станів чого-небудь, наприклад, одну з двох цифр або один з двох кольорів. Очевидно, що практична цінність такого носія є мінімальною.

Блок із 2 бітів може приймати один із 4 станів:

В 3-бітному блоці можна закодувати вже один із 8 станів:

Ну а 8-бітний блок може приймати аж 256 різних станів. Це вже досить істотна частинка двійкового коду, яка дозволяє відобразити один зі значної кількості варіантів.

Наприклад, кожним стану 8-бітного блоку можна співставити якусь літеру. Варіантів, а їх 256, буде достатньо для кодування усіх українських літер, включаючи строкові і прописні їх варіанти, а також усіх розділових знаків. Замінюючи кожну літеру відповідним 8-мибітним блоком, з двійкового коду можна скласти текст.

Цей принцип і використовується для запису в комп'ютері текстової інформації (детальніше про це йтиметься нижче).

Як бачте, 8-бітний блок має цілком реальну практичну цінність. Тому його й вирішили вважати мінімальною одиницею комп'ютерної інформації. Ця одиниця отримала назву байт.

Текстові файли складаються з сотень, тисяч або навіть десятків тисяч літер. Відповідно, для їх зберігання у двійковому коді потрібні сотні, тисячі або десятки тисяч байтів.

Тому на практиці частіше доводиться мати справу не з байтами, а з більшими одиницями:

• кілобайтами (1 кілобайт = 1024 байт);

• мегабайтами (1 мегабайт = 1024 кілобайт);

• гігабайтами (1 гігабайт = 1024 мегабайт);

• терабайтами (1 терабайт = 1024 гігабайт).

Кодування числової інформації

Для роботи з числовою інформацією ми користуємося системою числення, що містить десять цифр: 0 1 2 3 4 5 6 7 8 9. Ця система називається десятковою.

Окрім цифр, в десятковій системі велике значення мають розряди. Підраховуючи кількість чого-небудь і дійшовши до найбільшої із доступних нам цифр (до 9), ми вводимо другий розряд і далі кожне подальше число формуємо із двох цифр. Дійшовши до 99, ми змушені вводити третій розряд. В межах трьох розрядів ми можемо долічити вже до 999 і т.д.

Таким чином, використовуючи лише десять цифр і вводячи додаткові розряди, ми можемо записувати і проводити математичні операції з будь-якими, навіть найбільшими числами.

Комп'ютер веде підрахунок аналогічним чином, але має у своєму розпорядженні лише дві цифри - логічний нуль (відсутність у біта якоїсь властивості) і логічну одиницю (наявність у біта цієї властивості).

Система числення, що використовує тільки дві цифри, називається двійковою.

При підрахунку в двійковій системі вводити кожен наступний розряд доводиться значно частіше, ніж в десятковій.

Ось таблиця перших десяти чисел у кожній з цих систем числення:

Як бачте, в десятковій системі числення для відображення будь-якої з перших десяти цифр вистачає 1 розряду. У двійковій системі для тих же цілей знадобиться вже 4 розряди.

Відповідно, для кодування цієї ж інформації у вигляді двійкового коду потрібний носій місткістю щонайменше 4 біти (0,5 байта).

Людський мозок, який звик до десяткової системи числення, погано сприймає систему двійкову. Хоча обидві вони побудовані на однакових принципах і відрізняються лише кількістю використовуваних цифр. У двійковій системі так само можна здійснювати будь-які арифметичні операції із будь-якими числами. Головний її мінус - необхідність мати справу з великою кількістю розрядів.

Так, найбільше десяткове число, яке можна відобразити у 8 розрядах двійкової системи, - 255, в 16 розрядах - 65535, в 24 розрядах - 16777215.

Комп'ютер, кодуючи числа в бінарний код, користується двійковою системою числення. Але, залежно від особливостей чисел, може застосовувати різні алгоритми:

• невеликі цілі числа без знаку

Для збереження кожного такого числа на запам'ятовуючому пристрої, як правило, виділяється 1 байт (8 бітів). Запис здійснюється у повній аналогії з двійковою системою числення.

Цілі десяткові числа без знаку, збережені на носієві у двійковому коді, виглядатимуть приблизно так:

• великі цілі числа і числа зі знаком

Для запису кожного такого числа на запам'ятовуючому пристрої, як правило, відводиться 2-байтний блок (16 бітів).

Старший біт блоку (той, що крайній ліворуч) відводиться під запис знаку числа і в кодуванні самого числа участі не бере. Якщо число зі знаком "плюс", цей біт залишається порожнім, якщо зі знаком "мінус" - у нього записується логічна одиниця. Число ж кодується в інших 15 бітах.

Наприклад, алгоритм кодування числа +2676 буде наступним:

1. Перевести число 2676 з десяткової системи числення у двійкову. В результаті вийде 101001110100;

2. Записати отримане двійкове число в перші 15 бітів 16-бітного блоку (починаючи з правого краю). Останній, 16-й біт, повинен залишитися порожнім, оскільки кодоване число має знак +.

У результаті +2676 в двійковому коді на запам'ятовуючому пристрої виглядатиме так:

Слід зауважити, що у двійковому коді присвоєння числу від'ємного значення передбачає не лише зміну старшого біта. Здійснюється також інвертування усіх інших його бітів.

Щоб стало зрозуміло, розглянемо алгоритм кодування числа -2676:

1. Перевести число 2676 з десяткової системи числення в двійкову. Отримаємо двійкове число 101001110100;

2. Записати отримане двійкове число в перші 15 бітів 16-бітного блоку. Потім інвертувати, тобто, змінити на протилежне, значення кожного з 15 бітів;

3. Записати в 16-й біт логічну одиницю, оскільки кодоване число має від'ємне значення.

У результаті - 2676 на запам'ятовуючому пристрої у двійковому коді матиме наступний вигляд:

Запис від'ємних чисел в інвертованій формі дозволяє замінити усі операції віднімання, в яких вони беруть участь, операціями додавання. Це необхідно для нормальної роботи комп'ютерного процесора.

Максимальним десятковим числом, яке можна закодувати в 15 бітах запам'ятовуючого пристрою, є 32767. Іноді для запису чисел по цьому алгоритму виділяються 4-байтні блоки. У такому разі для кодування кожного числа використовуватиметься 31-бітів плюс 1 біт для кодування знаку числа. Тоді максимальним десятковим числом, що зберігається в кожному блоці, буде 2147483647 (зі знаком плюс або мінус).

• дробові числа зі знаком

Дробові числа на запам'ятовуючому пристрої в двійковому коді кодуються у вигляді так званих чисел з плаваючою комою (крапкою). Алгоритм їх кодування складніший, ніж розглянуті вище. Проте, спробуємо розібратися.

Для запису кожного числа з плаваючою комою комп'ютер найчастіше виділяє 4-байтний блок (32 біти):

• у старшому біті цього блоку (той, що крайній ліворуч) записується знак числа. Якщо число від'ємне, в цей біт записується логічна одиниця, якщо воно зі знаком "плюс" - біт залишається порожнім.

• у другому зліва біті аналогічним чином записується знак порядку (що таке порядок зрозумієте пізніше);

• у слідуючих за ним 7 бітах записується значення порядку.

• у 23 бітах, що залишилися, записується так звана мантиса числа.

Щоб стало зрозуміло, що таке порядок, мантиса і навіщо вони потрібні, переведемо в бінарний код десяткове число 6,25.

Порядок кодування буде приблизно таким:

1. Перевести десяткове число в двійкове (десяткове 6,25 рівне двійковому 110,01);

2. Визначити мантису числа. Для цього у числі необхідно змістити кому в потрібному напрямі, щоб зліва від неї не залишилося жодної одиниці. У нашому випадку кому доведеться перенести на три знаки вліво. У результаті, отримаємо мантису ,11001;

3. Визначити значення і знак порядку.

Значення порядку - це кількість символів, на яку була зміщена кома для отримання мантиси. У нашому випадку воно дорівнює 3 (чи 11 в двійковій формі);

Знак порядку - це напрям, у якому довелося зміщувати кому: ліворуч - "плюс", праворуч - "мінус". У нашому прикладі кома рухалася ліворуч, тому знак порядку - "плюс";

Таким чином, порядок двійкового числа 110,01 дорівнюватиме +11, а його мантиса ,11001. В результаті в двійковому коді на запам'ятовуючому пристрої це число буде записане таким чином:

Зверніть увагу, що мантиса в двійковому коді записується, починаючи з першого після коми знаку, а сама кома упускається.

Числа з плаваючою комою, закодовані в 32 бітах, називаю числами одинарної точності.

Коли для запису числа 32-бітового блоку недостатньо, комп'ютер може використовувати блок з 64 бітів. Число з плаваючою комою, закодоване в такому блоці, називається числом подвійної точності.

Бінарне кодування текстової інформації

Існує декілька загальноприйнятих стандартів кодування тексту в двійковому коді.

Одним з "найстаріших" (розроблений ще в 1960-х рр.) є стандарт ASCII (від англ. American Standard Code for Information Interchange). Це 7-бітний стандарт кодування. Тобто, використовуючи його, комп'ютер записує кожну літеру або знак в один 7-бітний блок запам'ятовуючого пристрою.

Як відомо, блок із 7 бітів може приймати 128 різних станів. Відповідно, в стандарті ASCII кожному з цих 128 станів відповідає якась літера, розділовий знак або спеціальний символ.

Подальший розвиток комп'ютерної техніки показав, що 7-бітний стандарт кодування є надто "тісним". У 128 станах, що приймаються 7-бітним блоком, неможливо закодувати літери усіх існуючих у світі писемностей.

Тому розробники програмного забезпечення почали створювати власні 8-бітні стандарти кодування тексту. За рахунок додаткового біта діапазон кодування в них був розширений до 256 символів. Щоб не було плутанини, перші 128 символів в таких кодуваннях, як правило, відповідають стандарту ASCII. Решта 128 - реалізують регіональні мовні особливості.

Восьмибітними стандартами, поширеними в нашій країні, є KOI8, UTF8, Windows1251 і деякі інші.

Розроблені також і універсальні стандарти кодування тексту (Unicode), що включають літери більшості існуючих мов. У них для запису одного символу може використовуватися до 16 бітів і навіть більше.

Існування великої кількості стандартів кодування тексту є причиною багатьох проблем. Ви, напевно, вже зустрічалися із ситуацією, коли в деяких програмах на екрані замість літер відображаються незрозумілі "кракозябри". Це тому, що комп'ютер іноді "помиляється" і невірно визначає кодування, в якому цей текст зберігається у його пам'яті.

У перспективі, ймовірно, буде прийнятий єдиний стандарт кодування тексту, який повністю враховуватиме різноманітність існуючих писемностей і на який поступово перейдуть усі комп'ютери, незалежно від локації і використовуваного програмного забезпечення. Але відбудеться це, судячи з усього, не скоро.

Кодування зображень у бінарний код

Щоб зберегти в двійковому коді фотографію, її спочатку віртуально розділяю на велику кількість дрібних кольорових крапок, які називаються пікселями (щось накшталт мозаїки).

Після розбиття на крапки колір кожного пікселя кодується у бінарний код і записується на запам'ятовуючому пристрої.

Перша цифрова фотокамера, створена в 1975 р. інженерами компанії Kodak, мала вагу 3 кг, робила чорно-білі знімки розміром 100Х100 пікселів і зберігала їх в бінарному коді на магнітну стрічку.
Запис одного знімка тривав довше 20 секунд.

Якщо говорять, що розмір зображення складає, наприклад, 512 х 512 крапок, це означає, що воно є матрицею, сформованою з 262144 пікселів (кількість пікселів по вертикалі, перемножена на кількість пікселів по горизонталі).

Приладом, який "розбиває" зображення на пікселі, є будь-яка сучасна фотокамера (у тому числі веб-камера, камера телефону) або сканер.

І якщо в характеристиках камери значиться, наприклад, "10 MegaPixels", значить кількість пікселів, на які ця камера розбиває зображення для запису в двійковому коді, - 10 мільйонів.

Чим на більшу кількість пікселів розділено зображення, тим реалістичніше виглядає фотографія в декодованому вигляді (на моніторі або після роздруковування).

Проте якість кодування фотографій залежить не лише від кількості пікселів, але й від їх колірної різноманітності.

Алгоритмів запису кольору в двійковому коді існує декілька. Найпоширенішим з них є RGB. Ця абревіатура - перші літери назв трьох основних кольорів: червоного - англ.Red, зеленого, - англ. Green, синього, - англ. Blue.

Зі шкільних уроків малювання, Вам, напевно, відомо, що змішуючи ці три кольори у різних пропорціях, можна отримати будь-який інший колір або відтінок.

На цьому і побудований алгоритм RGB. Кожен піксель записується в двійковому коді шляхом вказання кількості червоного, зеленого і синього кольору, що беруть участь в його формуванні.

Чим більше бітів виділяється для кодування пікселя, тим більше варіантів змішування цих трьох каналів можна використати і тим значнішою буде колірна насиченість зображення.

Колірна різноманітність пікселів, з яких складається зображення, називається глибиною кольору.

Якщо для кодування кожного пікселя якогось зображення виділяється 8 бітів двійкового коду, колірна різноманітність складе 256 кольорів.

Глибина кольору 12-бітів дасть 4096 кольорів, 16-бітів - 65536 кольорів, 18-бітів - 262144 кольорів.

Максимальна глибина кольору, що використовується в комп'ютерній техніці, - 24 біти. Таку глибину часто називають True Color ("Справжній колір"). Вона дозволяє відобразити близько 16,7 млн. кольорів. Око людини не здатне сприймати більшу їх кількість.

Проте, часто зустрічається й так звана 32-бітна глибина кольору. Вона не передбачає збільшення кількості відтінків. Додаткові біти, які виділяються для кодування кожного пікселя, призначені для регулювання ступеня його прозорості або ж не використовуються.

Описана вище техніка формування зображень з дрібних крапок є найпоширенішою і називається растровою. Але окрім растрової графіки, в комп'ютерах використовується ще й так звана векторна графіка.

Векторні зображення створюються тільки за допомогою комп'ютера (фотокамери цього робити "не вміють") і формуються не з пікселів, а з графічних примітивів (ліній, багатокутників, кіл та ін.).

Навіщо потрібна векторна графіка? У відомій дитячій пісеньці співається, що для зображення "чоловічка" достатньо намалювати всього дві "палки" й "огірочок". А уявіть, наскільки складно вручну скласти чоловічка з великої кількості крапок.

Векторна графіка - це креслярська графіка. Вона дуже зручна для комп'ютерного "малювання" і широко використовуються дизайнерами при графічному оформленні друкарської продукції, у тому числі створенні величезних рекламних плакатів, а також в інших подібних ситуаціях.

Векторне зображення в двійковому коді записується як сукупність примітивів із вказанням їх розмірів, кольору заливки, місця розташування на полотні і деяких інших властивостей.

Наприклад, щоб записати на запам'ятовуючому пристрої векторне зображення кола, комп'ютеру достатньо в двійковий код закодувати тип об'єкту (коло), координати його центру на полотні, довжину радіусу, товщину і колір лінії, колір заливки.

У растровій системі довелося б кодувати колір кожного пікселя. І якщо розмір зображення великий, для його зберігання знадобилося б значно більше місця на запам'ятовуючому пристрої.

Однак, векторний спосіб кодування не дозволяє записувати в двійковому коді реалістичні фото. Тому усі фотокамери працюють тільки за принципом растрової графіки. Рядовому користувачу мати справу з векторною графікою в повсякденному житті доводиться не часто.

Кодування звукової інформації

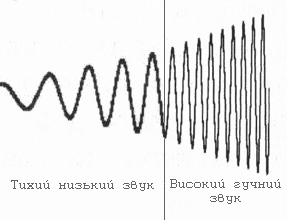
Будь-який звук, який чує людина, є коливанням повітря, що характеризується двома основними показниками: частотою і амплітудою.

Амплітуда коливань - це ступінь відхилення стану повітря від початкового при кожному коливанні. Вона сприймається нами як гучність звуку.

Частота коливань - це кількість відхилень стану повітря від початкового за одиницю часу. Вона сприймається як висота звуку.

Так, тихий комариний писк - це звук з високою частотою, але з невеликою амплітудою. Звук грози навпаки має велику амплітуду, але низьку частоту.

Якщо графічно зображувати звукову хвилю, вона виглядатиме таким чином:

Схему роботи комп'ютера зі звуком у загальних рисах можна описати так.

Мікрофон перетворює коливання повітря на аналогічні за характеристиками електричні коливання.

Звукова карта комп'ютера "вміє" перетворювати електричні коливання в двійковий код, який записується на запам'ятовуючий пристрій. При відтворенні такого запису відбувається зворотний процес (декодування) - двійковий код перетворюється в електричні коливання, які поступають в аудіосистему або навушники.

Динаміки акустичної системи або навушників мають протилежну мікрофону дію. Вони перетворюють електричні коливання на коливання повітря.

Але яким же чином звукова карта перетворює електричні коливання в двійковий код?

Якщо поглянути на графічне зображення хвилі і уважно проаналізувати її геометрію, можна побачити, що в кожен конкретний момент часу звук має певну інтенсивність (ступінь відхилення від початкового стану).

Отже, якщо весь відрізок часу, впродовж якого триває звук, розділити на дуже маленькі часові ділянки, то звукову хвилю можна буде записати як череду значень інтенсивності звуку у кожній такій часовій ділянці.

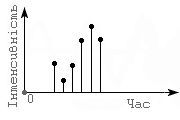
Але частота "дроблення" звуку має бути досить високою, інакше значення ділянок не відображатимуть реальну геометрію хвилі. Ось приклади надто низької частоти дроблення.

Описаний принцип розділення звукової хвилі на дрібні ділянки і лежить в основі двійкового кодування звуку.

Аудіокарта комп'ютера розділяє звук на дуже дрібні часові ділянки і кодує ступінь інтенсивності кожної з них в двійковий код. Таке "дроблення" звуку на частини називається дискретизацією. Чим вищою є частота дискретизації, тим точніше фіксується геометрія звукової хвилі і тим якіснішим виходить запис.

Так, проста мова (наприклад, диктофонний запис) нормально сприймається людиною, якщо частота дискретизації при кодуванні була не нижчою 8000 Гц (8КГц). Тобто, кожна секунда такого запису в двійковому коді повинна складатися як мінімум з 8000 частин.

Музичні ж твори, які зберігаються в комп'ютері, повинні мати ще вищу частоту дискретизації. При записі стандартних звукових CD вона складає щонайменше 44,1 КГц (44100 Гц).

Якість запису залежить також від кількості бітів, які використовуються комп'ютером для кодування кожної ділянки звуку, отриманої в результаті дискретизації.

Уявімо, наприклад, що для кодування кожної такої ділянки комп'ютер використовує 8 бітів. Як відомо, 8-бітний блок може приймати одне з 256 значень. Але раптом різноманітність інтенсивності ділянок, отриманих при дискретизації якогось звуку, виявилася ширшою (наприклад, 512 варіантів). У такому разі, комп'ютер "округлить" інтенсивність ділянок до найближчих доступних значень щоб "вкластися" в 256 варіантів і якість запису вийде низькою.

Кількість бітів, що використовуються для кодування кожної ділянки звуку, отримуваної при дискретизації, називається глибиною звуку.

Глибини звуку у 8-бітів вистачає для кодування простої мови. Але музичні твори з такою глибиною звучатимуть огидно. Тому значно частіше зустрічаються звукові файли, закодовані з глибиною 16, 24 або навіть 32 біти.

Слід враховувати, що далеко не всі пристрої, призначені для відтворення "цифрового" звуку, можуть працювати з файлами, закодованими з високою частотою дискретизації та/або великою глибиною звуку. Такі файли можуть відтворюватися на одному комп'ютері, і "не відкриватися" на іншому (якщо звукова карта не підтримує настільки високий рівень дискретизації або глибини звуку).

Особливості бінарного кодування відео

Відеозапис складається з двох компонентів: звукового і графічного.

Кодування звукової доріжки відеофайлу в двійковий код здійснюється за тими ж алгоритмами, що й кодування звичайних звукових даних (див. попередній пункт).

Принципи кодування відеозображення схожі з кодуванням растрової графіки (розглянуто вище), хоча й мають певні особливості.

Як відомо, відеозапис - це послідовність статичних зображень (кадрів), які швидко міняються. Одна секунда відео може складатися з 25 і більше картинок. При цьому, кожен наступний кадр лише трохи відрізняється від попереднього.

Враховуючи цю особливість, алгоритми кодування відео, як правило, передбачають запис лише першого (базового) кадру. Кожен же наступний кадр формується шляхом запису його відмінностей від попереднього.